

By Ethan Kuo
Face morphing is a technique used to transform one face into another. It involves blending the shape and appearance (texture) of two faces. In this project, we first morph one face into another through a gradual sequence. Then, we compute "average faces" for a population. Finally, we build a caricature by extrapolating features.
Suppose we want to morph these two faces: me and my favorite basketball player.


First, choose key points on both images that correspond to each other. Here, I do this manually. Note that each point uniquely coresponds to another point in the other image.


We then find the midpoints of each corresponding pair of key points to arrive at an average geometry. Essentially, this captures the average facial structure of the images. We then run the Delaunay triangulation algorithm on this average geometry to produce many triangles.
Why triangles? Because we can build a midway image by filling in the average geometry with color, triangle by triangle. Note that the triangulation can also be applied to each source image, meaning that every triangle in the average geometry corresponds to a triangle in each source image. The high level idea is that the color of each triangle will be the average color of the corresponding triangles in all source images.
More precisely, we will use inverse warping, which involves computing an affine transformation matrix that maps a triangle in the target geometry to the corresponding triangle in the source geometry. Then, we apply this matrix to each coordinate within the target triangle to get a corresponding pixel within the source triangle. Since this is a linear transformation, the preimage is not guaranteed to be an integer coordinate, so I used bilinear interpolation to assign a color to non-integer coordinates using its neighbors. Each pixel has a preimage in each source image, and we simply take the average RGB pixel value as its color.
Conceptually, I like to think of inverse warping as a way to peer into a source image and bring color into the target image.



Note for the midway face, we took the average of the geometries and the colors. We can generalize this using weighted averages to create intermediate faces. Combining them all, we arrive at a morph sequence!

Here are some more morph sequences I created! I think these ones are cleaner than the previous one because the source images are similar to begin with.









Here, I made a morph sequence between all 5 members of my family! The idea is similar to a 2-face morph, except I defined and triangulated separate correspondances for each adjacent pair of images, essentially stringing 4 morph sequences together.





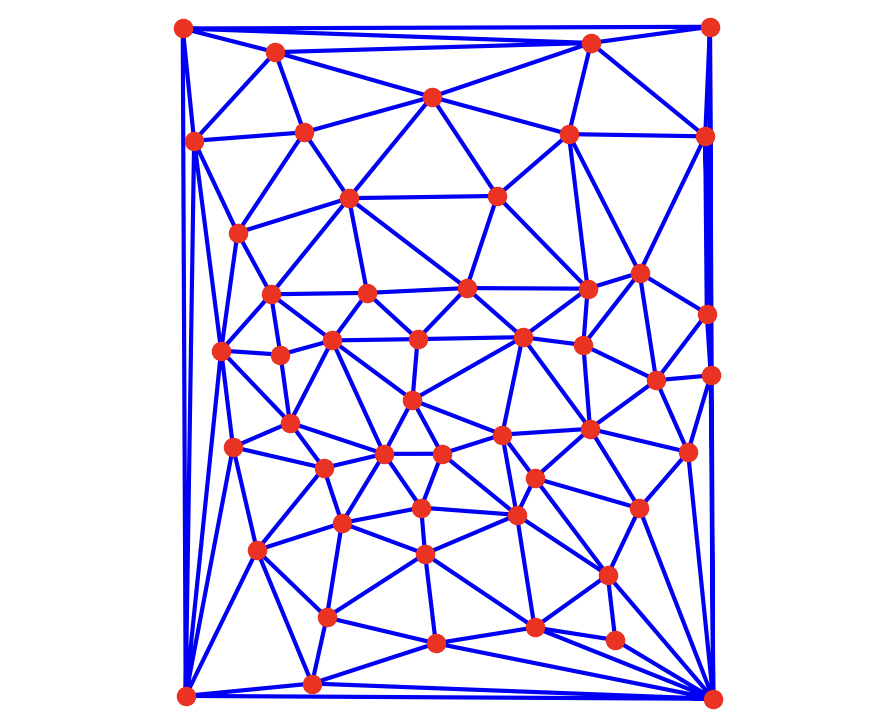
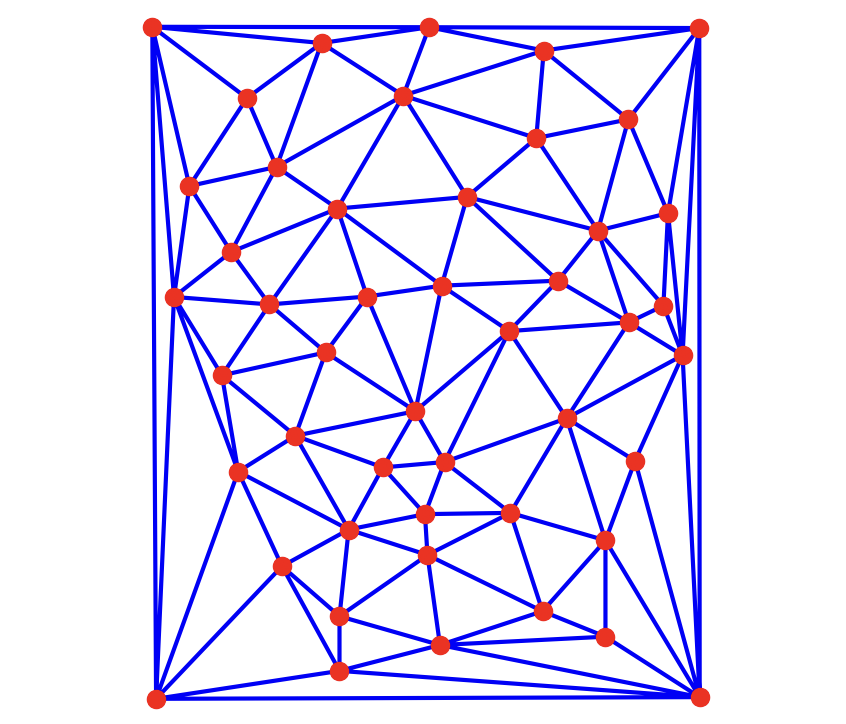
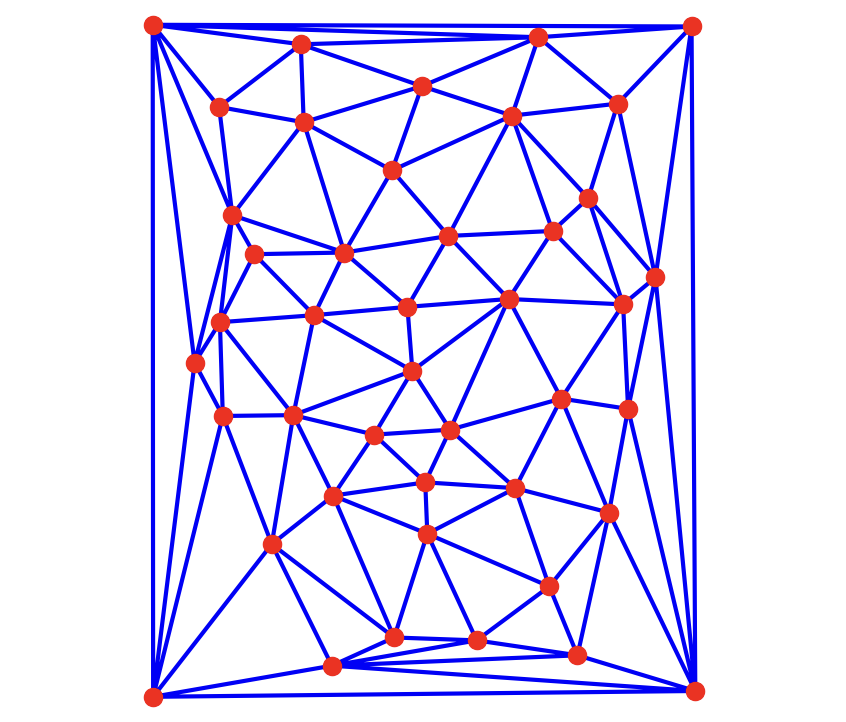

Using the FEI dataset, which consists of 400 faces of Brazilian people, we can compute an average face. This actually involves 2 averages: the average geometry, and the average texture. The average geometry is simply the sum of all geometries divided by the count. Then we bring texture into the mean geometry through inverse warping, equally combining pixel intensities from every face.


Here are examples of faces morphed into mean geometries.








For fun, I morphed myself into the average Brazilian neutral face geometry, and vice versa.


So far, we've only been interpolating between faces, or finding some intermediate between the two. We can also extrapolate between faces to accentuate unique features.
Here, I wanted to emphasize my own facial features relative to the average neutral face. Treating the
correspondences selected on my face as some vector p and the correspondences on the
average expression face as some vector q, I calculated p + α(p - q) as the
target
correspondences, computed the extrapolated triangulation, and then warped my face to these targets.
Intuitively, (p-q) is a bunch of difference vectors that each capture how much a feature deviates
from the mean. When we add some multiple of these vectors back into the image, we emphasize these deviations.

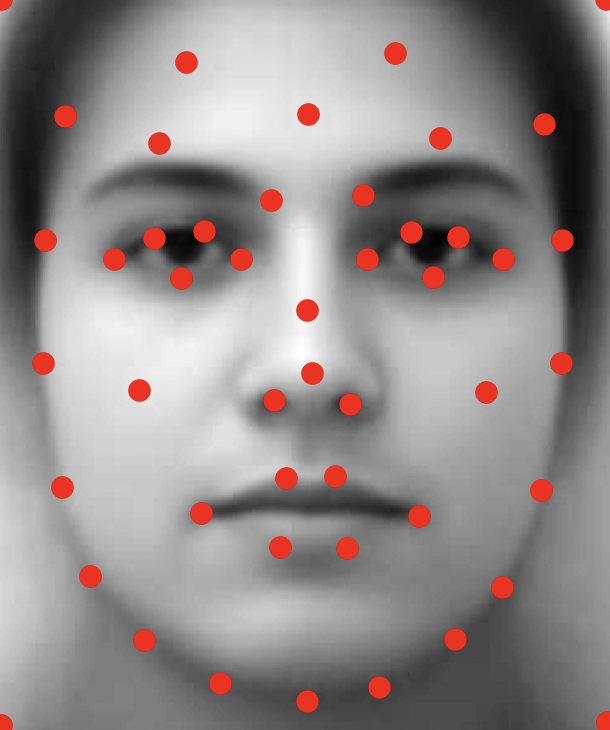
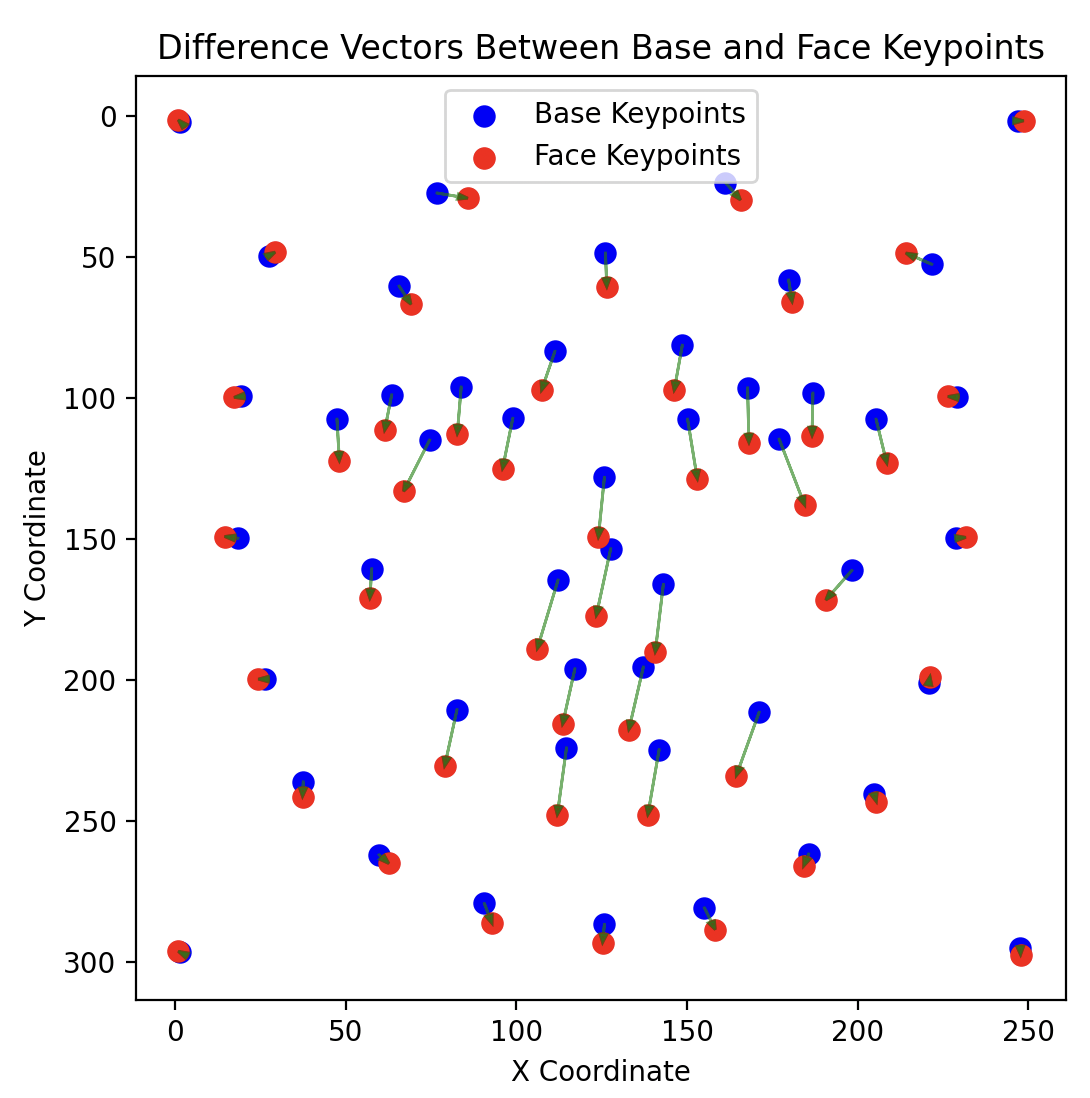





Here, you can see my unique features like a low nose and pointed eyes being exaggerated!